落とし穴
一つの例:要素編
この落とし穴の典型が要素の選び方で答が違うことです。
次の図は妥当な解です。(変位量は合っています)
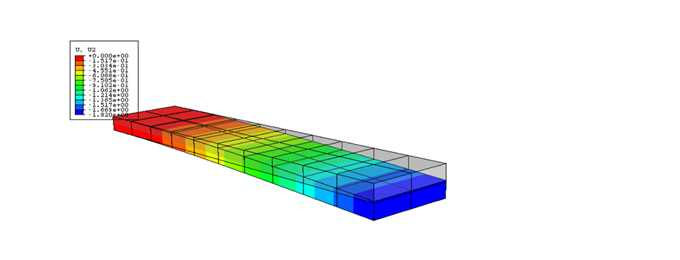
これを自動メッシュで切ると、次のようなメッシュになることがあります。
(ざっくり四面体で切りました。という表現です)

通常四面体要素は精度が悪いことは知られているので、さすがにこれを六面体で切り直します
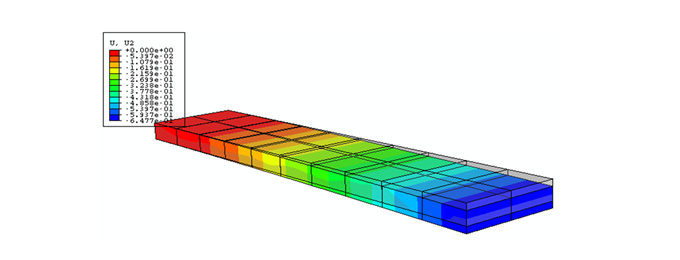
六面体でも適切な要素と不適切な要素があり、適切な要素を選べば最初のようにきちんとした答になりますが、間違った要素を選ぶと、この図のように不適切な答が出ます。
構造解析では要素選択に十分注意することが必要です。
なお、これらの出力も自動出力にすると、同じ変形が出て、数値だけが違うことになります。
もっと見つけにくい落とし穴になってしまいます。
もう一つの例:境界条件 (フック)
下のように壁にフックがねじ止めされていて、先端に荷重がかかっている問題があるとします。この時、この問題を構造解析するには、どんな点を考慮する必要がありますか?
(この考慮すべき点がすべて落とし穴になります。気づかないとおかしな解析をしてしまいます)
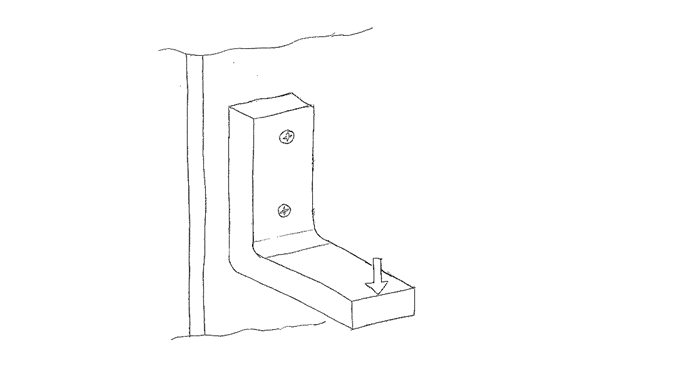
少なくとも、以下のような項目が考慮すべき項目となります
- 壁の剛性
- ねじの予張力
- 荷重の大きさ
- 荷重のかけ方
- 荷重のかかる回数
- フックの形状
- フックをモデル化する要素
- 要素の大きさ
- フックの壊れる値
- フックに許される変形量
- フックに許される応力
- ねじの剛性
- ねじの引き抜き強度
- 壁との接触状態
- フィレットの半径
- 壁の材質
- フックの材質
- ねじの材質
- そもそもどう壊れるか
- 変形の状態
どうですか? すべて気づきましたか?
問題によっては、気づいても 「これは影響無い」 という理由で考えなくても良い項目もあります。しかし、理由を持って考えないのと、思いつかないのでは、結果は同じでも、全く意味が違います。
この辺りが構造解析の難しいところです。
